APPENDIX A: VOICE LEADING OVERVIEW
Consonance and Dissonance
The way consonance and dissonance are treated is central to the way the whole of Western Music works and is the first concept to understand in the study of voice leading. It works on the assumption that consonant sounds are combinations of notes (intervals) that sound pleasant or melodious together whereas dissonant intervals sound harsh or unpleasant together.
Another way to express this is to say that consonant intervals create a feeling of stability whereas dissonant intervals create a feeling of instability that needs to be resolved. It is important to say that ideas of what constitutes consonance and dissonance have varied to some extent over time and vary from individual to individual. Also, it is important to say that most people perceive not just a simple binary division but a spectrum of consonance and dissonance varying from the most consonant intervals to the most dissonant intervals. The grouping below allows for this, to some extent, starting with the most consonant and ending with the most dissonant.
In 16th century polyphony, all musical intervals, involving two notes (within a span of an octave) are classified as consonant or dissonant according to the following list:
You will need to understand the naming and sounds of the musical intervals and the concept of "inversion" of intervals in order to follow this. Please refer to the books and website on basic theory in the bibliography
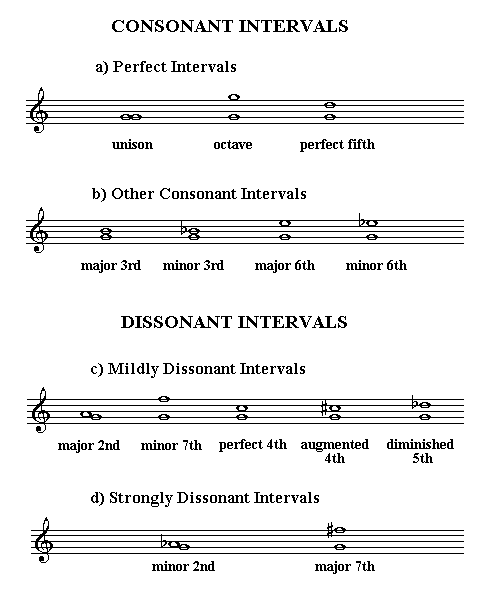
All of these intervals occur in the major and minor scales and in the scales of the modes.
I don't want to go into too much detail on the theory of consonance and dissonance here, but it's worth mentioning an interesting anomaly in the above classification. Inversions of intervals normally live within the same category. To "invert" an interval, take the lowest note and move it up an octave, above the upper note. For example, the minor 3rd is an inversion of the major 6th - both are considered to be consonant. However, whilst the interval of the perfect 4th is an inversion of the perfect 5th, the interval of the perfect 4th is treated as a dissonance, at least between any voice and the bass (It is treated as a consonance when between upper voices). Whereas, the perfect 5th is always treated as a consonance. The reasons for this anomaly are too complex to go into here. I may add more on the theory of consonance and dissonance to the website at a later date. For an historic discussion of this, see Zarlino and Helmholtz in the bibliography.
The following is a (made up) example of the simplest kind of two part voice leading, where the notes in both voices move at the same rate i.e. one note to one note. This is sometimes referred to as "first species" counterpoint.
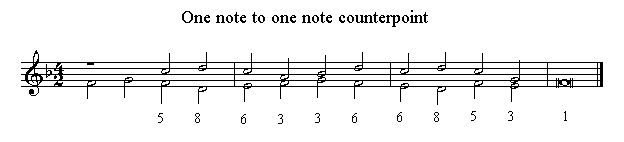
I've shown the intervals between the voices by numbers under each vertical note combination.
Whilst there is no rhythmic independence in this simple example, it does show melodic independence of the two parts - they move up and down independently - sometimes in contrary motion (in opposite directions) and sometimes in similar motion (moving in the same direction). - in this example, similar motion includes some parallel movement in 3rds and 6ths.
This highlights the basic components of this simplest type of counterpoint:
- Only consonant intervals are allowed in one note to one note voice
leading (first species).
- Perfect and non-perfect consonant intervals can be freely used.
I've included imitation - the second voice enters with the same melodic shape as the first voice but five notes higher. The upper voice thus imitates the lower voice but at a pitch that is more suited to its range. The imitation extends over the first 5 notes in each part. Imitation is an important contrapuntal device in 16th century polyphony. Each voice enters with the same tune or similar tune but at different times and at different pitches.
This example also illustrates the second major principle of voice leading: See the next section: The Independence of the Voices
Next Topic: The Independence of the Voices

