APPENDIX B: 20TH CENTURY POPULAR MUSIC
The Three Chord Trick
This section is best read in conjunction with the links to the main book section of this website. Whilst there are many good books and websites that describe chord progressions in popular music, what is unique about this website is that it describes the underlying principles which govern chord progressions in tonal music. By understanding these, the reader will be able to understand the wide range of tonal (and some modal) chord progressions possible and understand how these relate to musical phrases.
If you would like to read the full introduction to this appendix then please click here.
As an example of the basic tonal patterns as used in popular music, I will start off with a description of a melody based around three chords.
The three chord trick or three chord harmony is also a good way of understanding the origins of the tonal scales and a useful lead in to simple chord syntax. For more on the basics of tonality and related topics, please refer to the bibliography and web links section.
The three chord trick refers to the practice of accompanying a melody by only three chords. There are large numbers of melodies, both popular and classical, that can be harmonised in this way.
The three chords in question are not any combination of chords but are normally three specific chords that are referred to as: the tonic, subdominant and dominant chords of the key.
For example, in C major these are as follows:

These chords: C, F and G are all major chords and are referred to as the three primary chords in C major. Their roots are on the first, fourth, and fifth degrees of the musical scale which is why they are often referred to (using roman numerals) as chords: I, IV and V.
These chords are used because of certain important properties and relationships between them:
- In a major key, all three chords are major chords (made of a root, major 3rd and perfect 5th) and are the only major chords in the major key (excluding chromatic chords).
- The three chords are related by roots that are a 5th apart. G is a 5th higher than C and F is a 5th lower than C. The 5th relationship is important in chord progressions as will be seen in other parts of this website.
- The three chords, in combination, contain all the notes of the major scale, in fact they are the means of defining the major scale and of calculating the pitches of the notes in the natural 'just tempered' major scale.
- These chords are sufficient to harmonise any note of the major scale.
If we rearrange the notes of the three chords (by moving some down an
octave) then we can see how the major scale comes in to being:

C is from the C chord, D is from the G chord (an octave lower), E from the C chord, F from the F chord and so on.
In the minor key, in classical music, the three primary chords are related in a similar way. The difference is that the tonic and subdominant are usually minor but the dominant is usually altered to make it a major chord as in the major key. The reason the dominant is altered to major is to retain the leading note to tonic note relationship (B to C in C minor). This semitone relationship is an essential ingredient of the tonal system in both major and minor scales.

In a similar way, we can derive the minor 'harmonic' scale from these three chords as follows:

We can now examine the Bob Dylan song Blowing in The Wind. This will show that it is possible to compose a great song with only three chords and will show how chord progression structures work to create musical phrase structures.
We can demonstrate, with this example, all the main components of chord syntax. This is because the three primary chords not only contain all the notes of the major scale but are also capable of forming the essential ingredients of good chord progressions and musical phrase syntax, as I will show.
After a 2 bar tonic chord introduction, each verse of this song is made up of 32 bars, harmonised (in D major) as follows:

/ indicates the chord is repeated in the next barD is the tonic of the key (chord I as it occurs on the first degree of the scale)
G is the subdominant (chord IV as it occurs on the 4th degree of the scale) and
A is the dominant chord (chord V as it occurs on the 5th degree of the scale)
This pattern of chords is a good introduction to the theory presented in the whole of this website.
The sequence of chords is not random or arbitrary. It follows a clearly worked out system. The first line is made up totally of static harmony. Static harmony is harmony which does not move but oscillates around one chord. i.e. there is a movement from the tonic chord to another chord followed by a return to the tonic. Because the harmony here oscillates around the tonic it prolongs the tonic chord. This is the most common way of starting a musical phrase.
Using Roman numeral terminology, and showing the chord relationships (regardless of bars), this can be represented as follows:
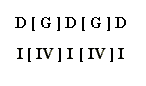
[ ] indicates an auxiliary chord, i.e. a chord which returns to the previous chord and consequently is used for creating static harmony.
Chord IV (the subdominant)
is the most popular auxiliary chord in popular music for forming static
harmony but other chords are used.
For more on static harmony see book Chapter 2.
The second line of the melody starts with 4 bars of identical static harmony but in the the last 4 bars of line 2, the pattern changes. These are not composed of static harmony but dynamic harmony. Here there is a chord progression rather than a mere oscillation as follows:
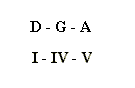
In dynamic harmony certain types of root progression are used in preference to other types of root progressions. In the above example the progression from I to IV is a progression involving the root of the chord rising an interval of a perfect 4th, i.e. D to G. This is the most common type of root progression used in dynamic harmony. The progression from IV to V is a progression of a rising 2nd (G to A) and is one of the other two root progressions normally used for dynamic harmony. The third type of root progression selected for dynamic harmony is the progression of a falling 3rd, however it is not possible to create a falling 3rd progression with just these 3 chords.
For more on dynamic harmony see Chapter 2.
An understanding of static and dynamic harmony is essential to understanding how phrase structures are constructed in tonal music. Lines 1 and 2 form a melodic unit which ends on chord V. The phrase starts with static harmony which is followed by dynamic harmony. Because the phrase does not end on the tonic, the result is an incomplete phrase which needs to be completed by a subsequent complete phrase. This type of incomplete phrase ends in an imperfect cadence (in this case, IV - V)
This is a very common incomplete phrase structure and can be represented using a 'parsing' diagram (similar to the types used to describe language syntax), as follows:
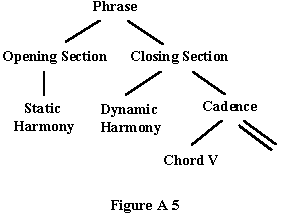
The double line shows that chord I is missing from the cadence. This kind of cadence is normally described as imperfect because the chord V does not return home to the tonic chord. The phrase is incomplete.
The third line of the melody is identical to the first line. (Melodically
it is the same too) It is made up totally of static harmony.
The fourth line is an altered version of the second line, but this time, it is made up totally of dynamic harmony and also ends in a perfect cadence (chord V to I)
This is a complete phrase and can be represented as follows
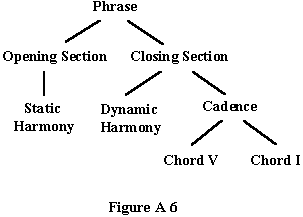
This structure represents the basic phrase structure for all tonal music. All other syntactic structures are derived from this basic structure. See Book Chapter 1.
The two phrases (the first incomplete and the second complete) conjoin to make up one complete unit. For a description of conjoining in language and other language structures see Chapter 1: Syntax in Language.
These four lines thus demonstrate all the components that make up the two most common type of phrase structure and illustrate the way chord patterns combine to create musical phrases.
It would be easy to stop here and say there is nothing else to say about the harmony of this piece but if we listen carefully to the guitar accompaniment we find there is an interesting line picked out. This can be shown, in harmonic outline, as follows:

The bar numbers refer to the bars starting at the first bar of the melody. The white notes are used to represent the important structural notes and the black notes represent passing notes. The beam is used to highlight the way the passing notes are connected.
The line we can hear goes: G - F# - E - D. Each of these notes is given emphasis highlighting their importance. This can be referred to as a linear progression because it moves step-by-step connecting one structural note to another.
This linear progression is made up of passing notes which connect the G of the G chord in bar 2 with the D of the D chord in bars 4 and 5. The passing notes F# and E are not consonant with the harmony notes.
The harmony initially moves from chord I to chord IV and the linear progression G - F# - E - D serves to emphasise the return from chord IV to chord I. In this instance, the linear progression does not generate any new chords but often linear progressions are accompanied by harmonies that create passing chords filling-in between structural (or Functional ) chords. When this kind of step-by-step filling in occurs in the bass part, in popular music, it is sometimes referred to as a 'walking bass' line.
Linear progressions are an important topic in tonal syntax for both popular music and classical music. An understanding of chord progression syntax requires an understanding of how both root progressions and linear progressions work.
Linear progressions are explained in more detail in Chapter 4 of the book section.
This example from Dylan conveniently introduces all the basic concepts
of chord progression syntax and harmonic phrase structures in tonal music.
For further details please refer to the rest of the book
outline in this website.
Next Section - The Blues Progression
Harmony in Popular Music Index
Ver 2.4a

